每日一练1

1.圆的面积

Description

给定圆的半径r，求圆的面积。

Format

Input

输入包含一个整数r，表示圆的半径。

Output

输出一行，包含一个实数，四舍五入保留小数点后7位，表示圆的面积。

Samples

输入数据 1

1
4

输出数据 1

1
50.2654825

Limitation

1s, 1024KiB for each test case.

解法：

  • 这里用到了一个重要的公式：acos();
  • acos()函数是cmath报头的库函数，它被用于查找给定数的反余弦的主值，它接受一个数字(x)和返回x的以弧度为单位的反余弦的主要值。
  • 注意：值( x )必须介于-1到+1之间，否则它将返回域错误( nan ).
  • acos(-1)是精准的π值

例如：

1
2
3
4
5
6
7
8
Input:
float x = 0.65;

Function call:
acos(x);    

Output:
0.863212
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
#include<cmath>
using namespace std;

int main(){
	
	double t=0,S;
	int r;
	scanf("%d",&r);
	t=acos(-1.0);
	S=t*r*r;
	printf("%0.7f",S);
	return 0;
}


2.Fibonacci数列

Description

Fibonacci数列的递推公式为：F_n = F_{n-1} + F_{n-2}F**n=F**n−1+F**n−2

已知： F_1 = = F_2 = 1F1==F2=1

Format

Input

输入包含一个整数n。(1<=n<=10000000)

Output

输出一行，包含一个整数，表示F_nF**n除以10007的余数。

Samples

输入数据 1

1
10

输出数据 1

1
55

hint

在本题中，答案是要求F_nF**n除以10007的余数，因此我们只要能算出这个余数即可，而不需要先计算出F_nF**n的准确值，再将计算的结果除以10007取余数，直接计算余数往往比先算出原数再取余简单。

Limitation

1s, 1024KiB for each test case.

解法

当使用正常方法时会导致超时oj无法通过如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//普通的递归：
#include<iostream>
using namespace std;
int fibon(int n){
	if(n<=2){
		return 1%10007;
	}
	return fibon(n-1)+fibon(n-2)%10007;
}
int main()
{
	int a,sum; 
	scanf("%d",&a);
	sum=fibon(a);
	printf("%d",sum);
	return 0;
	
}

image-20220209222230427

优化思想：

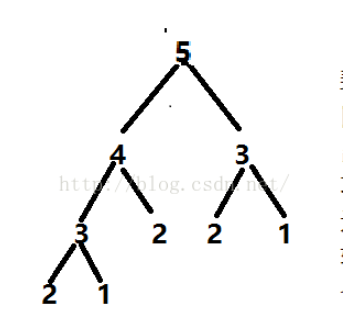
image-20220209222620422

在第五项斐波那切数列，首先得根据第一项和第二项算出第三项和第四项的数，而第三项先要算出第一项和第二项，第四项需要算出第二项和第三项，优化的思想在于如何避免重复的计算： 既然之前已经计算过那只需保存起来下次直接用就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
using namespace std;
int fibonac(int a,int b,int n)
{
	if(n > 2)
	{
		return fibonac(a+b,a,n-1);
	}
	return a;
}
int main()
{
	int n,a=1,b=1;
	scanf("%d",&n);
	int sum=fibonac(a,b,n);
	printf("%d",sum);
	return 0;
}

或:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<iostream>
using namespace std;
int main()
{ int f1=1,f2=1; 
int fn; int sum = 0; 
scanf("%d",&fn); 
if(fn<3)
{ printf("1");
 } 
else
{ 
for(int i=3; i<=fn; i++)
{ sum = (f1+f2)%10007; 
f1 = f2; 
f2 = sum; 
} 
printf("%d",sum); 
} 
return 0; 
}